Покерная математика на примерах

Давайте рассмотрим для чего игроку нужна покерная математика и как она поможет во время игры для просчета шансов и вероятностей на выигрыш.

Когда следует использовать покерную математику?

Покеристы применяют покерную математику, когда им требуется подсчитать шансы собственной руки на усиление, после чего принять решение, выгодно или нет им пытаться «поймать» ауты в отношении шансов банка. Участники принимают решение в зависимости от следующих факторов:

• Outs (ауты) – карты, способные вашу руку усилить.
• Pot Odds (шансы банка) – соотношение требуемой ставки от вас уже существующему поту.

Чтобы лучше понять принципы, рассмотрим математику покера на примерах.

NL 0.50/1.00 доллар:

• Hero (BU): король пики, девять пики.
• Raise 3 доллара.

SB: фолд:

• ВВ: колл 2 доллара.

На префлопе банк равен 6.50 долларов.

• Флоп: дама пики, восемь пики, два черви.
• ВВ: бет 3 доллара.

Математическое ожидание и Breakeven

Без понимания Breakeven и Expected Value (EV) покерная математика невозможна. Под EV понимается среднее ожидание покериста по выигрышу от следующей ставки. Математическое ожидание при этом просчитывается только на длительные дистанции.

Сравнивается EV с реальными итогами только после преодоления определенного количества партий. Даже при одной проигрышной раздаче, положительным остается математическое ожидание, значить игрок остается в плюсе.

Покерная математика определяет отрицательный и положительный EV – первый означает убытки, а второй дает выиграть. Breakeven означает точку безубыточности. Данная ставка не принесет ни выигрыша, ни победы.

Вся покерная математика игрока должна направляться на получение положительного EV. Его вероятность считается довольно просто: вероятность победы необходимо умножить на сумму ожидаемого выигрыша, после чего от полученного результата отнять вероятный денежный проигрыш, который умножен на шанс его выпадения.

Математика покера простыми словами выглядит таким образом: допустим, если ваш любимый футбольный клуб выигрывает в поединке, вы получите 1 доллар, но в случае проигрыша или ничьи столько же потеряете. Значение для вас имеют только такие события:

• Выигрыш клуба.
• Ничья/проигрыш.

Это вероятные итоги. Так как шанс на проигрыш или выигрыш из них принесет только один, вероятность победы и прибыли равна: вы получите 1 доллар выигрыша или аналогичную сумму потеряете. Это Breakeven – нулевой EV.

Если в случае победы вы получите менее 1 доллара, то будет отрицательный EV. В математике покера предусматривается постоянный выбор между отрицательным и положительным EV.

Ауты

Дисконтированные ауты

Покерная математика предусматривает такие способы расчета вероятности:

• Через шансы.
• Через вероятности.

Более проще запомнить первый способ. Математика покера для расчета шансов предлагается такие основные понятия:

• Шанс банка.
• Шанс выпадения аутов.

Рассчитывается шанс банка путем деления общей суммы банка (где ваш взнос отсутствует) на сумму ставки. После этого по приведенной ниже таблице можно оценить шансы выпадения аута на улицах флоп – терн, терн – ривер, ривер – флоп (при all-in на флопе). Покерная математика признает положительным EV только в ситуации, когда шансы банка значение вероятности выпадения аутов превышают.

Процесс дисконтирования аутов является довольно сложной процедурой, где самые опытные покеристы «сыплются». Этот процесс в покере основы математики полностью охватить не могут. Суть процесса состоит в том, что от общего количества ваших аутов необходимо отнять те, которые предоставляют сильную руку, а значит вероятность выигрыша для вашего оппонента.

К примеру, имея в «дырявом» стрите 234 идиотский конец (в этой ситуации – на руках туз), ваш аут, пятерку необходимо дисконтировать (сразу вычесть), так как такая комбинация способна легко противнику проиграть, если у него будет шестерка на руках. Постоянно необходимо дисконтировать ауты, с каждой новой улицы. Еще учитывайте поведение покеристов во время выпадения разных карт.

Просчет оддсов

Под оддсом понимается вероятность появление на следующей улице вашего аута. Вы можете для этого использовать приведенную выше таблицу, но в данной ситуации покерная математика предусматривает расчеты, основываясь на уже дисконтированных аутах.

На данном этапе игрок может допустить ошибку, если просчитает невнимательно на предыдущем этапе число дисконтированных аутов. Это соотношение шансов пота на ауты игрока на улице, следующей после дисконтирования.

В виде примера рассмотрим следующую ситуацию.

На скриншоте выше показан двусторонний стрейт-дро, где любая восьмерка или король дадут победную комбинацию и при первоначальных просчетах будут вашими аутами. Дисконтируя ауты и просчитывая оддсы, вам необходимо сделать определенные исключения. Если учесть, что ваша карта (девятка или семерка) станет идиотским концом стрейта, то это понизит вероятность выигрыша даже в ситуации, когда такой карты у противника нет.

Если зайдет король на следующей улице, то любым тузом будет бит ваш стрит. При выпадении 8-ки шансы снижаются вовсе – любой король или туз на руках вашу комбинацию бьет.

В данной ситуации из аутов необходимо вычесть 4-е восьмерки и отнять приблизительно два на вероятность туза на руках и выпадения на следующей улице короля. Смотреть следует на поведение оппонентов – если видно сильную комбинацию, то можно еще больше аутов дисконтировать.

Шансы банка

Под понятием шансов банка понимается сумма ставки относительно размера банка. При подсчете шансов банка требуется узнать, какое количество денег мы выиграть можем и какую сумму для этого нам следует поставить.

Допустим, на флопе общий банк: 6.50 долларов + 3 доллара (ставка противника) = 9.50 долларов. Hero должен доставить 3 доллара, чтобы просмотреть карту терна, а также выиграть потенциально 9.50 долларов.

Если исходить из этого, то шансы банка составляют 3 к 1. Чтобы в данной раздаче колл был «плюсовым», выиграть Hero должен только 1 раз из 3 (это 25% случаев).

Hero в данной ситуации должен контролировать, так как его шансы усилиться в данной раздаче шансы банка превышают. Действие будет «плюсовым» и выгодным на дистанции:

• Шансы на усиление составляют 48%.
• Для прибыльного колла нужные шансы банка составляют 25%.

Обратные шансы банка

При оценке своих шансов вы узнаете, с какой регулярностью и сколько вы выиграете, если «поймаете» нужные ауты своего дро. С помощью обратных шансов вы узнаете, сколько проиграете, если свое дро соберете, которое будет слабее, чем комбинации оппонента.

Расчет обратных шансов пота похож на расчет обычных шансов. Участники могут игру продолжить с обратными шансами банка, если достаточно выгодными будут ваши реальные пот-оддсы, но не имеет смысла вашу неготовую руку тянуть при отрицательных шансах.

Чтобы раздачу сыграть правильно с точки зрения математики покера, нужно выполнить такую последовательность действий:

• Определяем силу своей руки.
• Подсчитываем для усиления руки ауты.
• Часть своих аутов дисконтируем, если вы уверены, что они руку вашего оппонента помогут усилить.
• Подсчитываем шансы банка.
• Принимаем плюсовое решение.

Данный порядок действий для новичков может показаться довольно сложным, но с получением опыта вы сможете эти действия выполнять почти безошибочно и на автомате. Элементарная покерная математика вас быстро превратит из новичка в профессионала.

Таблица вероятности попадания различных стартовых рук в комбинацию на флопе

Игроку не нужно долго проводить расчеты с кучей формул в покерной математике. Достаточно использовать приведенную на скриншоте выше таблицу с уже готовыми расчетами.

В таблице видно, что собрать флеш одномастные карты помогают не всегда. Аналогично, только в 12% случаев пары в покере превращаются в сет, а не всегда выгодно разыгрывать младшие пары.

Математика покера может быть полезной для принятия решения на префлопе. Важно помнить, что в покере комбинация состоит из 5-ти, а не из 2-х карт. На скриншоте ниже показано, как события могут развиваться после флопа.

Шансы стартовых рук против конкретных рук оппонента

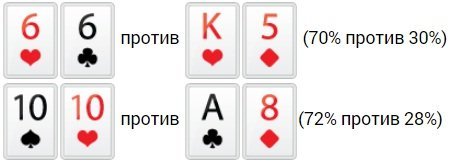
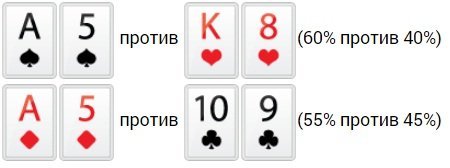
В игре важно представлять, какие у оппонента могут быть карты. Давайте рассмотрим, какие в Техасском Холдеме шансы имеют одни стартовые руки против иных определенных рук:

• Пара против другой маленькой пары.



• Пара против 2-х старших карт. Данная ситуация классическая. Ее часто можно увидеть во время игры в Холдем. Зачастую пара является фаворитом.



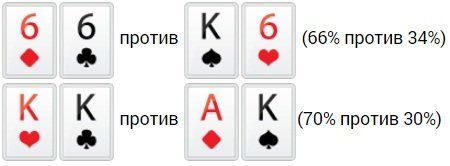
• Пара против двух младших. Здесь обычно пара считается фаворитом 5 к 1. Ситуация может поменяться, когда младшие карты являются коннекторами или одной масти.



• Пара против старшей и младшей карты. Примерно в 70% случаев пара считается фаворитом. Во время игры в покер против новичков подобная ситуация появляется очень часто.



• Пара против старшей карты, а также карты с номиналом, который равен карте в паре. Показан классический пример данной ситуации, когда сильная пара, к примеру, короли, противостоит АК. По факту у оппонента есть только 3 аута на туза (исключение – возможный флеш и стрит). Отсюда видно, что у королей есть 70% шансов на выигрыш.



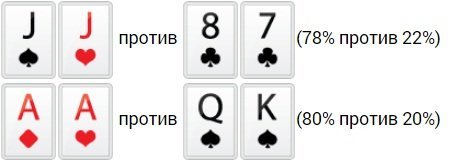
• Пара против маленькой карты и такой карты, номинал которой равняется карте в паре. Ситуация плюсовая, а для выигрыша противнику необходимо собрать минимум флеш, стрит или трипс, а под доминацией должна располагаться его старшая карта.



• Пара против коннекторов одной масти низкого достоинства. Некоторые игроки идут олл-ин с одномастными коннекторами. Зачастую происходит это из-за того, что довольно редко карты попадают под доминацию карт оппонента, а шансы на выигрыш выше, чем в прошлом примере, когда под доминацией находится одна из карт.



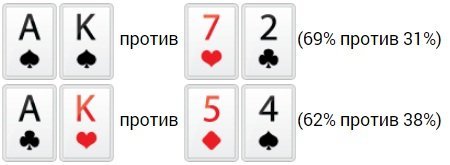
• Пара против коннекторов одной масти высокого достоинства. Когда на префлопе появляется подобная ситуация, то на победу шансы приблизительно одинаковы.



• 2-е старшие карты против 2-х младших карт. В данном случае младшие карты имеют на победу довольно неплохой процент, но зачастую все же будут проигрывать.



• Старшая карта против 2-х карт среднего достоинства. Здесь рука, которая в себя включает старшую карту, выше оценивается, чем рука соперника, но на выигрыш шансы не такие большие.



• Старшая карта против 1-ой карты среднего достоинства. В сравнении с прошлым примером, здесь возрастает процент на победу приблизительно на 5%. Старшая карта имеет на победу лучшие проценты.



• Доминируемая и старшая карта против доминированной и младшей карты. Здесь у оппонента только 3 аута (если пренебречь вероятными комбинациями флеш, стрит). В первой ситуации ему поможет только 7, а во втором – 3. При образовании у противника пары со старшей картой, выиграет ваша рука с идентичной парой, но со старшим кикером.



• Старшая карта и сильный кикер против такой старшей карты и слабым кикером. В Техасском Холдеме этот вариант очень часто встречается. Довольно важно иметь в покере хороший кикер в таких ситуациях для высоких шансов на выигрыш.

Все подсчеты дают приблизительное представление, что требуется делать с теми или иными картами во время разборок в покере с соперниками.